Bistable toggle switch

The simplest GRN exhibiting bistability can be modeled through two variables $x_1$ and $x_2$ that mutually repress each othe. We suppose that the system can be externally controlled by a chemical inducer that targets the synthesis rates of both genes. The model is defined as

\[\left\{ \begin{array}{l} \dot{x}_1 = -\gamma_1 x_1 + u(t) k_1 s^{-}(x_2,\theta_2) , \\ \dot{x}_2 = -\gamma_2 x_2 + u(t) k_2 s^{-}(x_1,\theta_1), \end{array}\right.\]

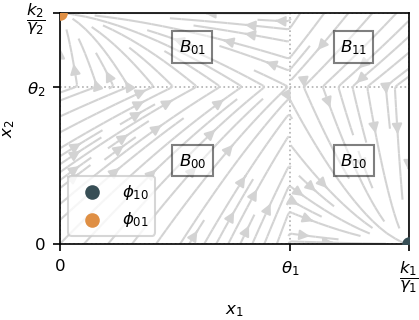
where a detail of each term can be found in Introduction. The domain $K=[0,k_1 / \gamma_1]\times [0,k_2 / \gamma_2]$ is forward invariant by the dynamics, which divides the state space into four regions:

\[\begin{array}{l} B_{00}=\left\{(x_1,x_2)\in \mathbb{R}^2 \mid 0<x_1<\theta_1, \ 0<x_2<\theta_2\right\},\\ B_{01}=\left\{(x_1,x_2)\in \mathbb{R}^2 \mid 0<x_1<\theta_1, \ \theta_2<x_2<\frac{k_2}{\gamma_2}\right\},\\ B_{10}=\left\{(x_1,x_2)\in \mathbb{R}^2 \mid \theta_1<x_1<\frac{k_1}{\gamma_1}, \ 0<x_2<\theta_2\right\},\\ B_{11}=\left\{(x_1,x_2)\in \mathbb{R}^2 \mid \theta_1<x_1<\frac{k_1}{\gamma_1}, \ \theta_2<x_2<\frac{k_2}{\gamma_2}\right\}, \end{array}\]

and two locally asymptotically stable steady states

\[\begin{align} \nonumber \phi_{10} &= \left(\frac{k_1}{\gamma_1},0\right)\in \bar{B}_{10}, \\ \nonumber \phi_{01} &= \left(0,\frac{k_2}{\gamma_2}\right)\in \bar{B}_{01}, \end{align}\]

as shown in the following figure:

The control objective is to induce a transition between an initial point in $B_{10}$ and a final value of $x_2$ in $B_{01}$, which can be written through the initial and terminal constraints:

\[ x(0) = x_0 \in B_{10}, \qquad x_1(t_f) < \theta_1, \qquad x_2(t_f) = x_2^f\]

for free final time $t_f > 0$ and for $x_2^f > \theta_2$.

Problem definition

using Plots
using Plots.PlotMeasures
using OptimalControl
using NLPModelsIpopt

We define the regularization functions, where the method is decided through the argument regMethod.

# Regularization of the PWL dynamics
function s⁺(x, θ, regMethod)
    if regMethod == 1 # Hill
        out = x^k/(x^k + θ^k)
    elseif regMethod == 2 # Exponential
        out = 1 - 1/(1 + exp(k*(x-θ)))
    end
    return out
end

# Regularization of |u(t) - 1|
function abs_m1(u, regMethod)
    if regMethod == 1 # Hill
        out = (u^k - 1)/(u^k + 1)
    elseif regMethod == 2 # Exponential
        out = 1 - 2/(1 + exp(k*(u-1)))
    end
    return out*(u - 1)
end

Definition of the OCP:

# Constant definition
k₁ = 1;
k₂ = 1     # Production rates
γ₁ = 1.4;
γ₂ = 1.6   # Degradation rates
θ₁ = 0.6;
θ₂ = 0.4   # Transcriptional thresholds
uₘᵢₙ = 0.6;
uₘₐₓ = 1.4   # Control bounds
x₀ = [0.65, 0.2]         # Initial point
x₂ᶠ = 0.55                # Final point
λ = 0.25                # Trade-off fuel/time

# Initial guest for the NLP
tf = 1.5
u(t) = 0
sol = (control=u, variable=tf)

# Optimal control problem definition
ocp = @def begin
    tf ∈ R, variable
    t ∈ [0, tf], time
    x = (x₁, x₂) ∈ R², state
    u ∈ R, control

    x(0) == x₀
    x₁(tf) ≤ θ₁
    x₂(tf) == x₂ᶠ

    uₘᵢₙ ≤ u(t) ≤ uₘₐₓ
    tf ≥ 0

    ẋ(t) == [
        - γ₁*x₁(t) + k₁*u(t)*(1 - s⁺(x₂(t), θ₂, regMethod)),
        - γ₂*x₂(t) + k₂*u(t)*(1 - s⁺(x₁(t), θ₁, regMethod)),
    ]

    ∫(λ*abs_m1(u(t), regMethod) + 1-λ) → min
end

Resolution through Hill regularization

In order to ensure convergence of the solver, we solve the OCP by iteratively increasing the parameter $k$ while using the $i-1$-th solution as the initialization of the $i$-th iteration.

regMethod = 1       # Hill regularization
ki = 50             # Value of k for the first iteration
N = 400
maxki = 200          # Value of k for the last iteration
while ki < maxki
    global ki += 50  # Iteration step
    local print_level = (ki == maxki) # Only print the output on the last iteration
    global k = ki
    global sol = solve(ocp; grid_size=N, init=sol, print_level=4*print_level)
end

▫ This is OptimalControl version v1.1.1 running with: direct, adnlp, ipopt.

▫ The optimal control problem is solved with CTDirect version v0.16.2.

   ┌─ The NLP is modelled with ADNLPModels and solved with NLPModelsIpopt.
   │
   ├─ Number of time steps⋅: 400
   └─ Discretisation scheme: trapeze

▫ This is OptimalControl version v1.1.1 running with: direct, adnlp, ipopt.

▫ The optimal control problem is solved with CTDirect version v0.16.2.

   ┌─ The NLP is modelled with ADNLPModels and solved with NLPModelsIpopt.
   │
   ├─ Number of time steps⋅: 400
   └─ Discretisation scheme: trapeze

▫ This is OptimalControl version v1.1.1 running with: direct, adnlp, ipopt.

▫ The optimal control problem is solved with CTDirect version v0.16.2.

   ┌─ The NLP is modelled with ADNLPModels and solved with NLPModelsIpopt.
   │
   ├─ Number of time steps⋅: 400
   └─ Discretisation scheme: trapeze

Total number of variables............................:     1605
                     variables with only lower bounds:        1
                variables with lower and upper bounds:      401
                     variables with only upper bounds:        0
Total number of equality constraints.................:     1204
Total number of inequality constraints...............:        1
        inequality constraints with only lower bounds:        0
   inequality constraints with lower and upper bounds:        0
        inequality constraints with only upper bounds:        1


Number of Iterations....: 199

                                   (scaled)                 (unscaled)
Objective...............:   9.1859086535922252e-01    9.1859086535922252e-01
Dual infeasibility......:   2.8330397637971917e-12    2.8330397637971917e-12
Constraint violation....:   5.2735593669694936e-15    5.2735593669694936e-15
Variable bound violation:   1.1365586916056714e-08    1.1365586916056714e-08
Complementarity.........:   1.0000000490263423e-11    1.0000000490263423e-11
Overall NLP error.......:   1.0000000490263423e-11    1.0000000490263423e-11


Number of objective function evaluations             = 215
Number of objective gradient evaluations             = 200
Number of equality constraint evaluations            = 215
Number of inequality constraint evaluations          = 215
Number of equality constraint Jacobian evaluations   = 200
Number of inequality constraint Jacobian evaluations = 200
Number of Lagrangian Hessian evaluations             = 199
Total seconds in IPOPT                               = 2.549

EXIT: Optimal Solution Found.

Plotting of the results:

plt1 = plot()
plt2 = plot()

tf = variable(sol)
tspan = range(0, tf, N)   # time interval
x₁(t) = state(sol)(t)[1]
x₂(t) = state(sol)(t)[2]
u(t) = control(sol)(t)

xticks = ([0, θ₁], ["0", "θ₁"])
yticks = ([0, θ₂, x₂ᶠ], ["0", "θ₂", "x₂ᶠ"])

plot!(
    plt1,
    x₁.(tspan),
    x₂.(tspan);
    label="optimal trajectory",
    xlabel="x₁",
    ylabel="x₂",
    xlimits=(θ₁/3, k₁/γ₁),
    ylimits=(0, k₂/γ₂),
)
scatter!(plt1, [x₀[1]], [x₀[2]]; label="x₀", color=:deepskyblue)
xticks!(xticks)
yticks!(yticks)
plot!(plt2, tspan, u; label="optimal control", xlabel="t")
plot(plt1, plt2; layout=(1, 2), size=(800, 300))

Resolution through exponential regularization

The same procedure for iteratively increasing $k$ is used.

regMethod = 2       # Exponential regularization
ki = 50             # Value of k for the first iteration
N = 400
maxki = 300          # Value of k for the last iteration
while ki < maxki
    global ki += 50  # Iteration step
    local print_level = (ki == maxki) # Only print the output on the last iteration
    global k = ki
    global sol = solve(ocp; grid_size=N, init=sol, print_level=4*print_level)
end

▫ This is OptimalControl version v1.1.1 running with: direct, adnlp, ipopt.

▫ The optimal control problem is solved with CTDirect version v0.16.2.

   ┌─ The NLP is modelled with ADNLPModels and solved with NLPModelsIpopt.
   │
   ├─ Number of time steps⋅: 400
   └─ Discretisation scheme: trapeze

▫ This is OptimalControl version v1.1.1 running with: direct, adnlp, ipopt.

▫ The optimal control problem is solved with CTDirect version v0.16.2.

   ┌─ The NLP is modelled with ADNLPModels and solved with NLPModelsIpopt.
   │
   ├─ Number of time steps⋅: 400
   └─ Discretisation scheme: trapeze

▫ This is OptimalControl version v1.1.1 running with: direct, adnlp, ipopt.

▫ The optimal control problem is solved with CTDirect version v0.16.2.

   ┌─ The NLP is modelled with ADNLPModels and solved with NLPModelsIpopt.
   │
   ├─ Number of time steps⋅: 400
   └─ Discretisation scheme: trapeze

▫ This is OptimalControl version v1.1.1 running with: direct, adnlp, ipopt.

▫ The optimal control problem is solved with CTDirect version v0.16.2.

   ┌─ The NLP is modelled with ADNLPModels and solved with NLPModelsIpopt.
   │
   ├─ Number of time steps⋅: 400
   └─ Discretisation scheme: trapeze

▫ This is OptimalControl version v1.1.1 running with: direct, adnlp, ipopt.

▫ The optimal control problem is solved with CTDirect version v0.16.2.

   ┌─ The NLP is modelled with ADNLPModels and solved with NLPModelsIpopt.
   │
   ├─ Number of time steps⋅: 400
   └─ Discretisation scheme: trapeze

Total number of variables............................:     1605
                     variables with only lower bounds:        1
                variables with lower and upper bounds:      401
                     variables with only upper bounds:        0
Total number of equality constraints.................:     1204
Total number of inequality constraints...............:        1
        inequality constraints with only lower bounds:        0
   inequality constraints with lower and upper bounds:        0
        inequality constraints with only upper bounds:        1


Number of Iterations....: 200

                                   (scaled)                 (unscaled)
Objective...............:   9.1716656538135588e-01    9.1716656538135588e-01
Dual infeasibility......:   1.9231944891600961e-10    1.9231944891600961e-10
Constraint violation....:   2.3586688158161451e-13    2.3586688158161451e-13
Variable bound violation:   1.1406815048076169e-08    1.1406815048076169e-08
Complementarity.........:   1.0000000602535572e-11    1.0000000602535572e-11
Overall NLP error.......:   1.9231944891600961e-10    1.9231944891600961e-10


Number of objective function evaluations             = 210
Number of objective gradient evaluations             = 201
Number of equality constraint evaluations            = 210
Number of inequality constraint evaluations          = 210
Number of equality constraint Jacobian evaluations   = 201
Number of inequality constraint Jacobian evaluations = 201
Number of Lagrangian Hessian evaluations             = 200
Total seconds in IPOPT                               = 2.714

EXIT: Optimal Solution Found.

Plotting of the results:

plt1 = plot()
plt2 = plot()

tf = variable(sol)
tspan = range(0, tf, N)   # time interval
x₁(t) = state(sol)(t)[1]
x₂(t) = state(sol)(t)[2]
u(t) = control(sol)(t)

xticks = ([0, θ₁], ["0", "θ₁"])
yticks = ([0, θ₂, x₂ᶠ], ["0", "θ₂", "x₂ᶠ"])

plot!(
    plt1,
    x₁.(tspan),
    x₂.(tspan);
    label="optimal trajectory",
    xlabel="x₁",
    ylabel="x₂",
    xlimits=(θ₁/3, k₁/γ₁),
    ylimits=(0, k₂/γ₂),
)
scatter!(plt1, [x₀[1]], [x₀[2]]; label="x₀", color=:deepskyblue)
xticks!(xticks)
yticks!(yticks)
plot!(plt2, tspan, u; label="optimal control", xlabel="t")
plot(plt1, plt2; layout=(1, 2), size=(800, 300))

This page was generated using Literate.jl.